BQ#7: Deriving the Difference Quotient

http://www.analyzemath.com/calculus/Differentiation/difference_quotient_1.gif

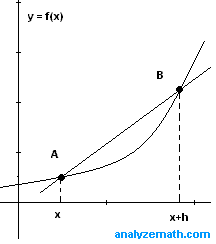
The formula for the  difference quotient comes from the original, algebraic equation for the slope of the line. When trying to find the slope of a tangent line (one intersection), we must also find the slope of a secant line (two intersections). When you plug in the values of the intersections and combine like terms in the denominator, we are left with with difference quotient.

Sources:

• http://www.analyzemath.com/calculus/Differentiation/difference_quotient_1.gif

BQ6: Unit U Concepts 1-2

1. A continuity is predictable; has no jumps, breaks and holes; and can be drawn without lifting a pencil. A discontinuity is an interruption in a graph. 

2. A limit is the intended height of a function. A limit exists when the limit and the value, the actual value of the function, are the same.

3. We evaluate limits numerically with a table, graphically by tracing the ends of a graph, and algebraically  is direct substitution.

BQ#4: Unit T Concept 3

A "normal" tangent graph appears to move uphill while a "normal" cotangent graph appears to move downhill because of the location of their asymptotes.

Reviewing what we learned earlier in this unit, we know that asymptotes appear wherever there is an undefined value. Furthermore, we learned that undefined answers are produced whenever we attempt to divide by zero.

In the Unit Circle, the ratio for tangent is "y/x" and the ratio for cotangent is "x/y". Where the denominator of "x" equals zero (pi/2 and 3pi/2) determines where the asymptotes for tangent are located. The same applies to where the value of "y" is equal to zero in a cotangent graph (0pi, pi, 2pi). 

BQ#3: Unit T Concepts 1-3

The graphs of sine and cosine are related to each of the other trig function graphs in the sense that they contain the measurements found within the Unit Circle. For secant and cosecant, we use the frame of a sine/cosine graph to draw the graphs in the shape of parabolas between the asymptotes. In tangent and cotangent graphs, it is evident that the shape of sine/cosine is depicted but simply cut in half by asymptotes.

BQ#5: Unit T Concepts 1-3

Sine and cosine do not have asymptotes because we are never going to divide by the value of zero sine "x" and "y". The value of "r" is always set equal to 1 in the Unit Circle. The ratio for sine is "y/r" and the ratio for cosine is "x/r". In the other trig functions, there is a possibility that the denominators "x" and "y" can be valued at zero.

BQ#2: Unit T: Introduction to Trig Graphs

Trig graphs are similar to the Unit Circle in the sense that they both possess the values of the quadrants. The period for sine and cosine is 2π because the sign of the function changes with every two quadrants. The period for tangent and cotangent is π because the sign of the functions changes with every other quadrant.

The fact that sine and cosine have amplitudes of 1 as seen in the Unit Circle means that they start at zero, or the origin of a coordinate plane. Since the other trig functions have amplitudes outside the values of the Unit Circle means that the entirety of their graphs shifts along the y-axis accordingly.

BQ #1: Unit P Concepts 2, 4 & 5: Law of Sines (SSA) & Area Formulas

2. Law of Sines 

 

Why is SSA ambiguous? Accurately draw the triangles that would be associated with one of these problems (pick any from the SSS or PQ). Connect your answer to your knowledge of Unit Circle trig function values.

SSA is ambiguous because we are only given one of the three angles as opposed to two in ASA or AAS. Because of this, there is the chance that we may get an answer of one, two, or no possible triangles.

5. Area Formulas

 Show that our “traditional” area formula of A=1/2bh, the area of an oblique triangle, and Heron’s area formula will result in the same values. Draw and label a right triangle with angles of 35* and 65*. Have the base be 4 units. Find all the remaining pieces using your knowledge of this chapter and then find the area using all three area formulas.

Our "traditional" area formula, the area of an oblique triangle, and Heron's area formula will all result in the same value for the area of a triangle.