Inquiry Activity Summary
The objective of the activity below was to derive or obtain the patterns of special right triangles from equilateral shapes, in this case a larger triangle and a square. The benefits of completing this task is that it provides us with another means of identifying the Unit Circle values.
 |
| Activity page 1 of 2. Click to enlarge. |
 |
| Activity page 2 of 2. Click to enlarge. |
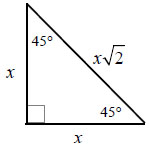
45°, 45°, 90° Triangle
 |
| http://www.gradeamathhelp.com/image-files/45-45-90-triangle.jpg |
As shown in the Step 1 of the above activity (see page 1), the process of deriving a 45°, °45, 90° congruent triangles of the desired angles. We label the hypotenuse of the smaller triangles "c", and we can label the two legs "a" and "b". Based on what we informed in this activity, we know that the side lengths of the square were valued at 1; thus, both "a" and "b" are equal to 1. To find the value of the hypotenuse, we can use the Pythagorean Theorem (a² + b² = c²). By plugging in the corresponding values, we get c= √2. We can then collectively use the newly-obtained values and a variable (e.g. "n") to triangle from a square first involves the act of dividing, or breaking down, the initial shape. To do so, we slice the square diagonally to from two form a general pattern. This means that by adding a variable to each of the values, the pattern becomes applicable to a square with any given side length!
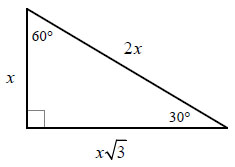
30°, 60°, 90° Triangle
 |
| http://www.gradeamathhelp.com/image-files/30-60-90-triangle.jpg |
In Step 2 of the activity (see page 2), we are presented with an equilateral triangle with a side length of 1. Referring back to what we have learned in Geometry, we know that a triangle with sides of equal length is also equiangular, meaning that each of the three angles are 60°. To begin this step, me must again breakdown the shape by dividing it into congruent parts--this time by drawing a vertical line through the middle. Again we label out hypotenuse "c" and the two legs of the shape "a" and "b". Using the given information, we know that "a" is equal to 1/2 and "c" is equal to 1. As you may have probably already guessed from Step 1, we use the Pythagorean Theorem to find the missing height. By plugging in the respective values into the equation and solving for "b", we get the answer of √3 /2. In order to translate our values into the normal pattern without fractions, we multiply each of them by 2. By doing so, "a" becomes 1, "b" becomes √3, and "c" becomes 2. As stated before, we can include a variable
(e.g. "n") to our answers to form a general pattern. This allows the pattern to be applicable to an equilateral triangle with any given side length!
Inquiry Activity Reflection
Something I never noticed before about special right triangle is that they can be joined together to form larger, equilateral and equiangular shapes!
Being able to derive these patterns myself aids my learning because it enables me to identify patterns that could prove useful in future practice and exams.
Works Cited
- http://www.gradeamathhelp.com/image-files/45-45-90-triangle.jpg
- http://www.gradeamathhelp.com/image-files/30-60-90-triangle.jpg



